Để làm tốt các bài tập hình học không gian nhất định bạn phải biết các xác định góc giữa đường thẳng và mặt phẳng để khi đọc đề bài có thể dễ dàng vẽ hình và tính toán. Nhiều bạn gặp khó khăn trong vấn đề này, chính vì vậy TKBooks sẽ chia sẻ cách cách xác định góc giữa đường thẳng và mặt phẳng trong không gian để bạn học có thể nắm rõ và áp dụng trong quá trình học.
I. Cách xác định góc giữa đường thẳng và mặt phẳng trong không gian
Đối với chuyên đề này bạn cần nắm được lý thuyết khái niệm về góc giữa đường thằng và mặt phẳng cùng với phương pháp xác định.
1. Định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian
Góc giữa đường thằng và mặt phẳng là góc giữa đường thằng và hình chiếu vuông góc của nó trên mặt phẳng.
2. Cách xác định góc giữa đường thẳng và mặt phẳng trong không gian
* Với góc vuông: Nếu đường thằng vuông góc với mặt phẳng thì góc giữa đường thẳng và mặt phẳng là 90 độ

* Với góc thông thường:
Để xác định góc giữa đường thẳng ( không phải là góc vuông) cần thực hiện theo các bước sau:
– Tìm điểm chung giữa đường thẳng và mặt phẳng
– Tìm hình chiếu của một điểm thứ 2 trên mặt phẳng rồi từ đó tìm được hình chiếu của đường thẳng và tìm được góc
Ví dụ cụ thể:
Cách dựng hình chiếu vuông góc của điểm M đến mặt phẳng (P)
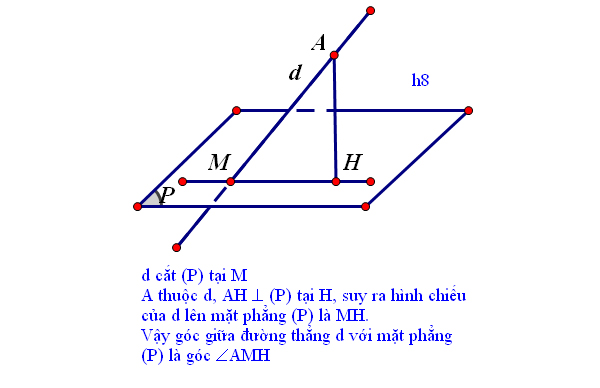
Thực hiện như sau:
– Nếu có đường thẳng d vuông góc với mặt phẳng (P). Kẻ đường MH song song với đường thẳng d thì H là hình chiếu vuông góc của M trên H (P)
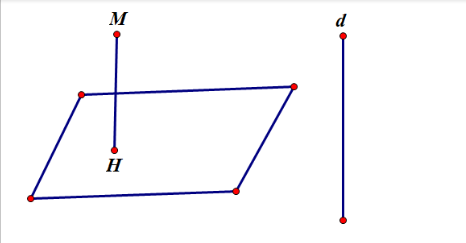
Ta có: HM // d, d ⊥ (P ) ⇒ MH ⊥ (P), H là hình chiếu vuông góc của M trên (P)
– Nếu như không có sẵn đường thẳng vuông góc thì thực hiện như sau:
Chọn mặt phẳng (Q) chứa điểm M sao cho mặt phẳng (Q) vuông góc với mặt phẳng (P)
Từ M kẻ MH vuông góc với giao tuyến a thì H là hình chiếu vuông góc của M trên (P)
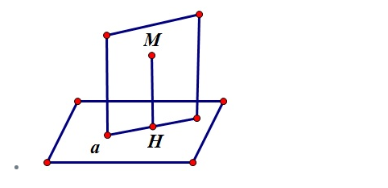
Cách tính góc thường gặp: đó là sử dụng hệ thức lượng trong tam giác vuông
Tòm tắt về cách xác định góc giữa đường thẳng và mặt phẳng trong không gian: Điều quan trọng nhất để xác định góc tạo giữa đường và mặt phẳng đó là xác định giao điểm. Rồi từ điểm còn lại tung 1 nét vẽ vuông góc tới mặt phẳng và cắt mặt phẳng tại 1 điểm giả sử là điểm H. Đem nối H với giao điểm. Và góc cần tìm nằm ngay chính giao điểm đó.
II. Hướng dẫn xác định góc trong hình học không gian
Việc xử lý hình trong bài toán hình học không gian bao gồm 3 bước:
+ Dựng hình : đã được hướng dẫn tại :
+ Xác định góc:
– Đường thẳng với mặt phẳng
-Mặt phẳng với mặt phẳng
+ Độ dài các cạnh
Ở note này, mình sẽ hướng dẫn các bạn việc xác định góc trong hình học không gian
1. Góc giữa đường thẳng và mặt phẳng bất kì
Gỉa thiết. Cho AB cắt (P) tại A, tìm gọi tạo bờiAB và (P).
B1: Xác định giao điểm của AB và (P) => Điểm A (các bạn nên khoanh tròn giao điểm bằng bút chì )
B2: Từ B hạ BH vuông góc với (P)
B3: Nối HA
=> Góc HAB là góc tạo bởi (P) và AB

Ví dụ 1: Cho bài toán SABC, SA vuông góc với đáy. Tam giác ABC vuông tại A. Xác định góc tạo bởi SB và SAC
Bài giải:
Bước 1: Cần xác định S là giao điểm của SB và (SAC)
Bước 2: Từ B kẻ 1 đt vuông góc SAC đó chính là AB
Vậy góc BSA chính là góc cần tìm.

Chứng minh:
+ Ta có: AB vuông góc SA (SA vuông góc với đáy)
và AB vuông góc AC (giả thiết)
Suy ra: AB vuông góc (SAC)
Vậy: SA là hình chiếu vuông góc của SB trên (SAC)
và góc ASB là góc tạo bởi SB và (SAC)
2.
II. Góc giữa mặt phẳng với mặt phẳng
Gỉa thiết: Cho (P) và (Q) giao nhau tại giao tuyến AB. Tìm góc giữa (P) và (Q)
B1: Xác định giao tuyến của (P) và (Q) => AB
B2: từ P lấy 1 điểm M bất kì, kẻ MH vuông góc mặt phẳng (Q)
B3: từ H kẻ HK vuông góc với AB
B4: Nối MK, ta được MKH là góc tạo bởi (P) và (Q)
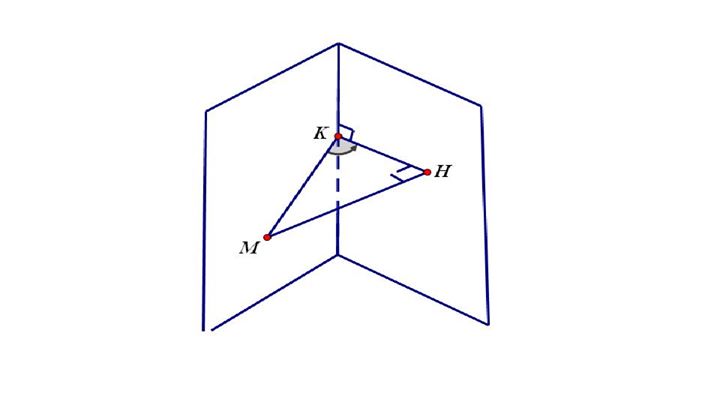
Ví dụ: Góc tạo bởi mặt bên với mặt bên
Cho chóp SABCD, SA vuông với đáy, góc tạo bởi (SAB)và (SBC) là 60o. ABCD là hình bình hành. Xác định góc tạo bởi (SAB) và (SBC)
(Vì viết trên facebook nên sẽ k có các kí hiệu vuông góc,song song, ngoặc hệ, em nào muốn chép thì tự kí hiệu lại nhé)
Hướng dẫn:
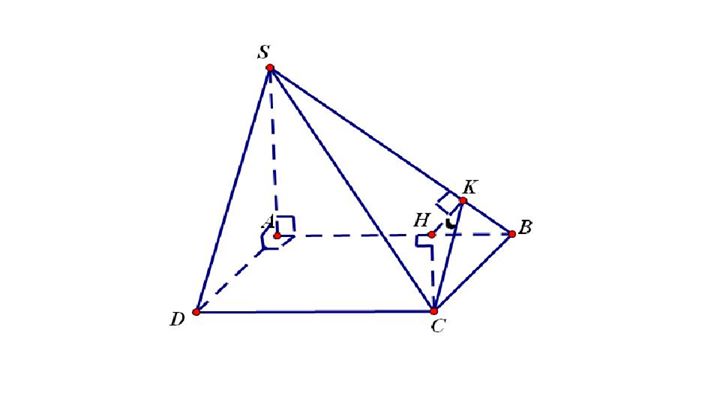
-Cách làm:
B1: Xác định giao tuyến là của 2 mp là SB
=> Vậy ở mặt phẳng (SAB) ta còn điểm A, mặt phẳng(SBC) ta còn C
Lời khuyên: Nên hạn chế chọn chân đường cao của chóp để kẻ đường cao đến mp còn lại (kinh nghiêm bản thân)
B2: Từ C kẻ CH vuông góc AB
Tại sao có thể biết trước việc CH vuông góc với mặt phẳng (SAB) , mình sẽ giải thich kĩ ở 1 note sau.
B3: Từ H kẻ HK vuông góc SB
-Trình bày
-Vẽ:
từ C kẻ CH vuông góc AB
từ H kẻ HK vuông góc SB
Nối CK
-Chứng minh
+Ta có:
CH vuông góc AB (1)
CH vuông góc SA ( SA vuông góc với đáy) (2)
Từ (1) và (2) => CH vuông góc với (SAB)
+Ta có:
HK vuông góc SB (3)
CH vuông góc SB (4)
Từ (3) và (4) => SB vuông góc (CHK)
=> SB vuông góc CK
+Ta có
(SAB) giao (SBC) tại SB
CK vuông góc SB
HK vuông góc SB
=> góc HKB = góc tạo bảo (SAB) và (SBC) = 60 độ
Chú ý:
-Sau khi xác định giao tuyến của 2 mặt phẳng, chúng ta còn chừa ra 2 điểm nằm trên mỗi một mặt ( như bài toán vừa rồi, (SAB) giao (SBC) tại SB => còn điểm A ở (SAB) và C ở (SBC).
– Hãy chọn điểm không phải là chân đường cao. VD như trong bài là điểm C để kẻ vuông góc tới mặt phẳng còn lại.
-Tóm tắt: Để xác định góc tạo bới mặt phẳng với mặt phẳng:
B1: Xác định giao tuyến
B2: Từ 1 trong 2 điểm còn lại trên mỗi mặt phẳng, tung 1 nét vẽ vuông góc tới mặt phẳng kia. Cắt mặt phẳng kia tại H
B3: Từ H kẻ HK vuông góc tới giao tuyến
B4: Nối K với điểm đã chọn. Góc cần tìm nằm tại K
II. Bài tập cách xác định góc giữa đường thẳng và mặt phẳng trong không gian có lời giải
Biết cách xác định góc giữa đường thẳng và mặt phẳng trong không gian bạn có thể áp dụng làm các bài tập sau:
Bài tập 2: Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với cạnh đáy, SA = 3a. Tính góc giữa đường thẳng và mặt phẳng trong các trường hợp sau:
1. SB và (ABCD)
2. SC và (ABCD)
3. SC và (SAB)
Bài giải:

Góc đường thẳng SB và mặt phẳng (ABCD)
SB ∩ (ABCD) = B → hình chiếu vuông góc của B trên (ABCD) là B ( B – điểm chung của đường thẳng SB và mp (ABCD).
SA ⊥ (ABCD) → Hình chiếu vuông góc của S trên (ABCD) là A
⇒ Hình chiếu vuông góc của SB trên (ABCD) là AB. Góc giữa SB và (ABCD) là góc SBA ( điểm chung nằm giữa)
Tam giác SAB vuông tại A. tanSBA = SA/AB = 3.
Góc giữa đường thẳng SC và mặt phẳng (ABCD)
SC ∩ (ABCD) = C → hình chiếu vuông góc của C trên (ABCD) là C ( B – điểm chung của đường thẳng SB và mp (ABCD).
SA ⊥ (ABCD) → Hình chiếu vuông góc của S trên (ABCD) là A
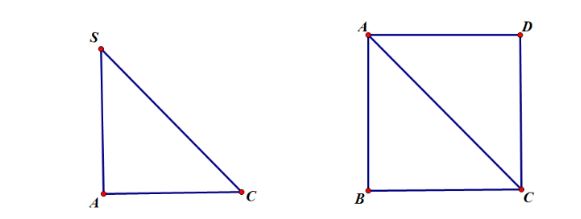
tan SCA = SA / AC
Xét hình vuông ABCD áp dụng định lí pitago cho tam giác vuông ABC ta có AC2= AB2 + BC2
Góc giữa đường thẳng SC và mặt phẳng (SAB)
SC ∩ (SAB) = S → hình chiếu vuông góc của S trên (SAB) là S ( S – điểm chung của đường thẳng SC và mp (SAB).
Cần tìm hình chiếu vuông góc của C trên mặt phẳng (SAB)
SA ⊥ (ABCD) → SA ⊥ BC, AB ⊥ BC → BC ⊥ (SAB) ⇒ B là hình chiếu vuông góc của C trên (SAB)
⇒ Hình chiếu vuông góc của SC trên (SAB) là SB. Góc giữa SC và (SAB) là góc BSC ( điểm chung nằm giữa)
Tam giác SBC vuông tại B. tanBSC = BC/SB.
⇒ Hình chiếu vuông góc của SC trên (ABCD) là AC. Góc giữa SC và (ABCD) là góc SCA ( điểm chung nằm giữa)
Tam giác SAC vuông tại A.
III. Bài tập cách xác định góc giữa đường thẳng và mặt phẳng trong không gian tự giải
Bài tập 1: Hình chóp S.ABCD,đáy là hình thang vuông tại A và SA vuông góc với đáy, có AD=2BC=2AB=2a,SA=a. Tính góc giữa:
a. Các cạnh bên của hình chóp với mặt đáy (ABCD)
b. SB,SC với mặt bên (SAD)
Bài tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và SA = a√2.
a. Gọi AH là đường cao của tam giác SAB . Chứng minh rằng AH vuông góc với mặt phẳng (SBC) và tính AH .
b. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD) .
c. Gọi O là giao điểm của AC và BD . Tính khoảng cách từO đến mặt phẳng (SBC)
Bài tập 3: Cho lăng trụ ABC.A/B/C/ ,ABC là tam giác vuông cân,AB=BC=a;B/A=B/B=B/C=a.Tính góc giữa B/B với mặt phẳng (ABC) và mặt phẳng (B/AC)
Bài tập 4: Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , mặt bên SAB là tam giác đều và SC = a√2. Gọi H và K lần lượt là trung điểm của các cạnh AB và AD
a. Chứng minh rằng: SH vuông góc với (ABCD)
b. Chứng minh rằng: AC vuông góc với(SHK)
Bài tập 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SA = a , SB = a√3 và mặt phẳng (SAB) vuông góc với mặt phẳng đáy . Gọi M , N lần lượt là trung điểm của các cạnh AB , BC . Tính theo a thểtích của khối chóp S.BMDN và tính cosin của góc giữa hai đường thẳng SM , DN
Bài tập 6: Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a , SA = a vuông góc với đáy (ABCD) . Hãy:
a. Chứng minh các mặt bên của hình chóp là tam giác vuông .
b. Tính cosin góc nhị diện (SBC,SDC)
Những chia sẻ về cách xác định góc giữa đường thẳng và mặt phẳng trong không gian rất cụ thể cùng với bài tập ví dụ đi kèm chắc chắn sẽ rất hữu ích cho bạn trong quá trình học tập môn toán. Các bạn chú ý ôn tập nhiều hơn để đạt được kết quả học tập như mong muốn nhé! Chúc các bạn học tốt!











