Trong tổng hợp công thức tính diện tích tam giác 60s.edu.vn sẽ cùng các bạn, các em học sinh đi tìm hiểu sự khác biệt trong cách tính diện tích tam giác trong trường hợp như tam giác thường, cân, đều hoặc vuông
Các em học sinh chắc chắn không thể quên những công thức toán học quan trọng khi áp dụng vào các bài tập , ví dụ như công thức tính diện tích tam giác, hình vuông, hình bình hành…Tuy nhiên trong mỗi hình, đặc biệt hình tam giác lại có nhiều cách tính diện tích tam giác khác nhau, ví dụ như cách tính diện tích tam giác thường sẽ khác so với khi tính diện tích tam giác vuông, cân hoặc đều.
Như vậy việc phân tách rõ ràng giữa các công thức tính diện tích tam giác chắc chắn sẽ hỗ trợ rất nhiều cho các bạn học sinh, sinh viên khi tiếp cận với những bài toán liên quan đến hình tam giác.
TỔNG HỢP CÁCH TÍNH DIỆN TÍCH TAM GIÁC: THƯỜNG, VUÔNG, CÂN, ĐỀU
Để dễ hình dung hơn, TKBOOKS sẽ hướng dẫn các bạn cách tính diện tích hình tam giác theo thứ tự từ tổng quan, phổ biến tới chi tiết để các bạn dễ hình dung hơn nhé.
1. Công Thức Tính Diện Tích Tam Giác Thường Trong Toán Học
– Diện tích tam giác thường được tính bằng cách nhân chiều cao và độ dài đáy, sau đó chia cho 2. Diện tích tam giác thường sẽ bằng 1/2 tích của chiều cao và chiều dài cạnh đáy tam giác.
– Công thức tính diện tích tam giác thường: S = (A . H)/ 2
Trong đó:
+ a: Chiều dài đáy tam giác (đáy là một trong 3 cạnh của tam giác theo cách đặt của người tính)
+ h: Chiều cao của tam giác, phần đáy chiếu lên (chiều cao bằng đoạn thẳng hạ từ đỉnh xuống đáy, và vuông góc với đáy của một tam giác).
– Suy ra: H= (Sx2)/ A hoặc a= (Sx2)/ H
Cho một hình tam giác ABC, trong đó có chiều cao nối từ đỉnh xuống đáy BC bằng 3 cm, chiều dài đáy BC là 6 cm. Tính diện tích tam giác thường ABC?
Gọi a =6 và h=3.
Suy ra S = (a x h)/ 2 = (6×3)/2 hoặc 1/2 x (6×3) = 9 cm
Trường hợp không cho cạnh đáy hoặc chiều cao, mà cho trước diện tích và cạnh còn lại, hãy áp dụng công thức suy ra ở trên để tính toán.

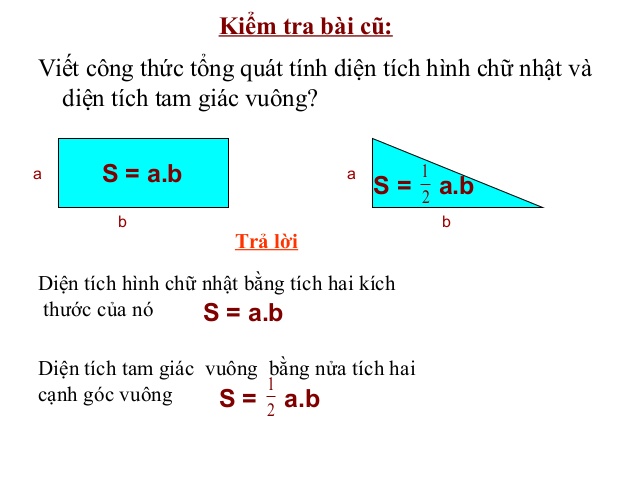
2. Công Thức Tính Diện Tích Tam Giác Vuông Trong Toán Học
– Công thức tính diện tích tam giác vuông giống cách tính diện tích tam giác thường, bằng 1/2 tích của chiều cao với chiều dài đáy. Hình tam giác vuông sẽ khác biệt hơn so với tam giác thường do có rõ chiều cao và chiều dài cạnh đáy học sinh không cần vẽ thêm để tính chiều cao tam giác.
– Công thức tính diện tích tam giác vuông: S = (A X H)/ 2
+ h: Chiều cao của tam giác, ứng với phần đáy chiếu lên
+ a: Chiều dài đáy tam giác vuông (đáy là một trong 3 cạnh của tam giác và vuông góc với một cạnh đáy)
– Suy ra: H=(Sx2)/ A hoặc A= (Sx2)/ H
Tam giác vuông ABC, vuông góc tại điểm B, cạnh đáy BC là 5 cm, chiều cao 2 cm. Diện tích của hình tam giác vuông ABC bằng bao nhiêu? Đơn vị tính: cm.
Gọi a =5 và h=2.
Suy ra S = (a x h)/ 2 = (5×2)/2 hoặc 1/2 x (5×2) = 5 cm
3. Công Thức Tính Diện Tích Tam Giác Cân
Tam giác cân là tam giác có hai cạnh bên và hai góc bằng nhau. Cách tính diện tích tam giác cân cũng tương tự cách tính tam giác thường, nếu bạn biết chiều cao tam giác và cạnh đáy.
Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác tới cạnh đáy tam giác, rồi chia cho 2.
– Công thức tính diện tích tam giác cân: S = (A X H)/ 2
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
+ a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
Cho tam giác cân ABC có chiều cao nối từ đỉnh A xuống BC bằng 7 cm, chiều dài BC là 6 cm. Tính diện tích của tam giác cân ABC ?
Gọi a =6 và h=7.
Suy ra S = (a x h)/ 2 = (6×7)/2 hoặc 1/2 x (6×7) = 21 cm
4. Công Thức Tính Diện Tích Tam Giác Đều Trong Toán Học
Tam giác đều là tam giác có 3 cạnh bằng nhau, mỗi góc trong tam giác đều có góc bằng 60 độ, bất cứ tam giác nào có ba góc bằng nhau cũng được coi là tam giác đều.
– Công thức diện tích tam giác đều: S = A2 X (√3)/4
+ a: chiều dài một cạnh trong tam giác đều.
Có một tam giác đều ABC với chiều dài cạnh bằng nhau là 9 cm, biết các góc của tam giác này đều 60 độ. Hỏi diện tích tam giác đều ABC bằng bao nhiêu?
Do mỗi cạnh AB = AC = BC = 9 nên chiều dài cạnh a = 9.
S = a2 x (√3)/4 = S = 92 x (√3)/4 = 81 x (√3)/4 = 81 x (1,732/4) = 35,07 cm
Ngoài ra còn nhiều cách tính diện tích tam giác khác người dùng biết được tất cả các cạnh, như sử dụng công thức Heron, tính diện tích tam giác bằng góc và hàm lượng giác.
Dù sử dụng công thức tính diện tích tam giác nào đi chăng nữa các bạn, các em cần hiểu rằng, không phải lúc chiều cao cũng nằm trong tam giác, cần vẽ thêm một chiều cao và cạnh đáy bổ sung. Quan trọng khi tính diện tích tam giác, chú ý chiều cao phải ứng với cạnh đáy nơi nó chiếu xuống.
Đã có rất nhiều công cụ hỗ trợ người dùng, đặc biệt là các em học sinh trong việc tính toán, một số phần mềm hỗ trợ tính toán tính diện tích tam giác phổ biến như SpeQ Mathematics, Calculatormatik, Magiccalc, download CocCoc giải toán,…nhiều người thường tính toán bằng Fxcalc Chức năng CocCoc giải toán khá tiện dụng và hiệu quả.