Bài toán viết phương trình đường thẳng đi qua 2 điểm A và B khi biết trước tọa độ của chúng lớp 9 có rất nhiều bạn học sinh hỏi và nói rằng chưa biết làm dạng này. Bên cạnh đó đây cũng là một dạng toán có thể rơi vào đề thi tuyển sinh vào lớp 10. Vì vậy mà 60s.edu.vn sẽ hướng dẫn bạn dạng bài viết phương trình đường thẳng đi qua 2 điểm cùng với một số bài tập đi kèm để bạn có thể nắm rõ dạng bài này và ôn tập tốt.
1. Cách viết phương trình đường thẳng đi qua 2 điểm
1.1. Cách 1:
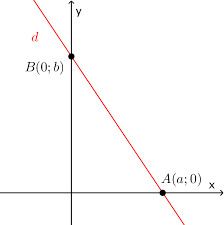
Giả sử 2 điểm A và B cho trước có tọa độ là: A(a1;a2) và B(b1;b2)
- Gọi phương trình đường thẳng có dạng d: y=ax+b
- Vì A và B thuộc phương trình đường thẳng d nên ta có hệ
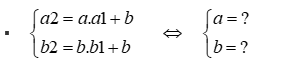
- Thay a và b ngược lại phương trình đường thẳng d sẽ được phương trình đường thẳng cần tìm.
1.2. Cách 2 giải nhanh
Tổng quát dạng bài viết phương trình đường thẳng đi qua 2 điểm: Viết phương trình đường thẳng đi qua 2 điểm A(x1;y1) và B(x2;y2).
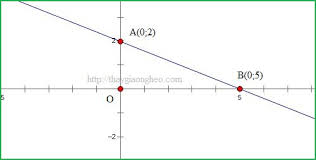
Cách giải:
Giả sử đường thẳng đi qua 2 điểm A(x1;y1) và B(x2;y2) có dạng: y = ax + b (y*)
Vì (y*) đi qua điểm A(x1;y1) nên ta có: y1=ax1 + b (1)
Vì (y*) đi qua điểm B(x2;y2) nên ta có: y2=ax2 + b (2)
Từ (1) và (2) giải hệ ta tìm được a và b. Thay vào sẽ tìm được phương trình đường thẳng cần tìm.
Bài tập ví dụ viết phương trình đường thẳng đi qua 2 điểm
Bài tập 1: Viết phương trình đường thẳng đi qua hai điểm A (1;2) và B(0;1).
Bài giải:
Gọi phương trình đường thẳng là d: y=ax+by=ax+b
Vì đường thẳng d đi qua hai điểm A và B nê n ta có:
⇔ 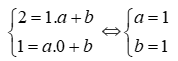
Thay a=1 và b=1 vào phương trình đường thẳng d thì d là: y=x+1
Vậy phương trình đường thẳng đi qua 2 điểm A và B là : y=x+1
Bài tập 2: Cho Parabol (P):y=–ײ . Viết phương trình đường thẳng đi qua hai điểm A và B biết A và B là hai điểm thuộc (P) và có hoành độ lần lượt là 1 và 2.
Bài giải
Với bài toán này chúng ta chưa biết được tọa độ của A và B là như nào. Tuy nhiên bài toán lại cho A và B thuộc (P) và có hoành độ rồi. Chúng ta cần đi tìm tung độ của điểm A và B là xong.
Tìm tọa độ của A và B:
Vì A có hoành độ bằng -1 và thuộc (P) nên ta có tung độ y =−(1)²=–1 => A(1;−1)
Vì B có hoành độ bằng 2 và thuộc (P) nên ta có tung độ y =–(2)²=−4 ⇒ B(2;−4)
Gọi phương trình đường thẳng cần tìm có dạng d: y=ax+b
Vì đường thẳng d đi qua hai điểm A và B nê n ta có:
⇔ 
Thay a=-3 và b=2 vào phương trình đường thẳng d thì d là: y=−3x+2
Vậy phương trình đường thẳng đi qua 2 điểm A và B là: y=−3x+2
Chú ý: Hai điểm A và B có thể biết trước tọa độ hoặc chưa biết tọa độ ngay, chúng ta cần phải đi tìm tọa độ của chúng.
2. Cách giải các dạng bài phương trình đường thẳng đi qua 2 điểm
Cần phải có kiến thức căn bản về cách viết phương trình đường thẳng đi qua 2 điểm thì mới có thể có cách giải cụ thể cho từng bài tập được. Với phương trình đường thẳng đi qua 2 điểm:
2.1 Đường thẳng (d) đi qua điểm A(xo;yo) và có VTCP u(a;b)
Ta có phương trình tham số là x = xo + at ; y = yo + at ( trong đó t thuộc R), nếu ta có a#0 và b#0 thì được phương trình chính tắc là: (x-xo)/a = (y-yo)/b
2.2. Đường thẳng (d) đi qua điểm A(xo;y0) và có VTPT n(a;b)
Ta có tổng quát là a(x-xo) + b(y-yo) = 0.
2.3. Đường thẳng (d) đi qua điểm A(xo;yo) và có hệ số góc k
Ta có phương trình y = k(x-xo) + yo với k = tana (a là góc tạo bởi đường thẳng (d) và tia Ox. Cách xác định giá trị k: Đường thẳng đi qua 2 điểm B(x1;y1) ; C(x2;y2) thì có hệ số góc là k = (y2 – y1) / (x2 – x1)
– Ta có: VTPT và VTCP vuông góc nhau nên tích vô hướng của chúng = 0, vì vậy nếu có VTPT n(a;b) thì sẽ suy ra đc VTCP là u(-b;a) và ngược lại.
– Nếu đề bài đã cho 2 điểm A và B thì VTCP chính là vecto cùng phương với vecto AB.
2.4: Cách viết phương trình đường thẳng (d) đi qua 2 điểm A;B trong không gian Oxyz
– Tính![]()
– Viết PT đường thẳng đi qua A hoặc B, và nhận![]() làm vtcp
làm vtcp
VD: Viết phương trình tham số, chính tắc của đường thẳng (d) đi qua hai điểm A(-1;3;-2); B(4;2;-3)
Giải:
![]()
Phương trình tham số:
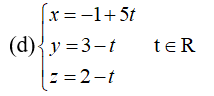
Phương trình chính tắc:
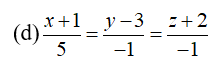
2. Bài tập ứng dụng viết phương trình đường thẳng đi qua 2 điểm
Bài tập 1: Viết phương trình y = ax + b của đường thẳng:
a) Đi qua điểm A(4; 3), B(2;- 1)
b) Đi qua điểm A(1;- 1) và song song với Ox
Bài giải:
a). Phương trình đường thẳng (d) qua A(4; 3) và B(2;- 1) có dạng tổng quát là y = ax + b, trong đó a, b là các hằng số cần xác định.
Vì A(4; 3) ∈ d nên ta có phương trình của (d), do đó ta có: 3 = a.4 + b.
Tương tự B(2;- 1) ∈ d nên ta có: – 1 = a.2 + b
Từ đó ta tìm được phương trình đường thẳng AB là: y = 2x – 5.
Phương trình đường thẳng AB là: y = 2x – 5.
b). y = – 1.

Bài tập 2: Viết phương trình dạng y = ax + b của đường thẳng đi qua hai điểm M(-1;3) và N(1;2)
Bài giải:
Vì đường thẳng có phương trình dạng y = ax + b nên ta cần xác định các hệ số a và b.
Đường thẳng đó đi qua M(-1;3) và N(1;2), tức là tọa độ M và N thỏa mãn phương trình y = ax + b.
Đường thẳng đi qua M(-1;3) và N(1;2) nên ta có:
-a + b = 3 và a + b = 2
Giải ra ta có : a=-1/2 ; b=5/2
Vậy phương trình đường thẳng là: y = (-1/2)x + 5/2
Bài tập 3: Viết phương trình đường thẳng (d) đi qua 2 điểm A(1;2) và B(3;4).
Ta có: vecto AB = (3 – 1; 4 – 2) = (2;2)
Chọn u(1;1) là VTCP của đt(d) (lấy như vậy để tinh gọn tính toán sau này).
vậy VTPT của (d) là n(-1;1).
– Phương trình tham số của (d): x = 1 + t ; y = 2 + t (t thuộc R).
– Phương trình tổng quát (d): (-1)(x-1) + 1(y-2) = 0 <=> x – y + 1 = 0.
– Phương trình chính tắc (d): (x-1)/(-1) = (y-2)/1.
– Phương trình theo hệ số góc:
Hệ số góc của đường thẳng (d) k = (4-2)/(3-1) = 2/2 = 1.
Vậy phương trình đường thẳng(d): y = 1(x-1) + 2 <=> y = x+1.
Bài tập rèn luyện cách viết phương trình đường thẳng đi qua 2 điểm A. B

Trên đây là một ví dụ nhỏ thôi, trong quá trình làm bài thì đề bài sẽ có nhiều thay đổi, các bạn linh hoạt để có các giải phù hợp nhé!
Học toán cũng cần phải có sự kiên trì thì mới có thể học tốt lên được. Kiên trì ôn tập và làm các dạng toán. Hy vọng những chia sẻ về cách viết phương trình đường thẳng đi qua 2 điểm trên cùng với một số bài tập hướng dẫn đi kèm sẽ giúp ích cho bạn trong quá trình học tập, chúc các bạn học tốt!











