Trước khi bước vào hình học tọa độ không gian, thì đây là những công thức cần thiết của phương pháp tọa độ mà các bạn cần nằm lòng.
– Bài viết được sắp sếp rất khoa học và dễ nhớ. Hi vọng sẽ giúp ích được các e. (Nên dùng sơ đồ tư duy để hình vẽ hóa nó, giúp đạt hiệu quả ghi nhớ tối đa)
I. Phần lý thuyết về các công thức cần thiết của phương pháp tọa độ
Cho
- Phép cộng trừ véc tơ.

– Cho hai điểm A(xA, yA, zA) và B(xB, yB, zB). Khi đó
![]()
- Modul của 1 vec tơ (hay còn gọi là độ dài vec tơ):
![]()
![]()
3. Tích vô hướng của 2 véc tơ là 1 số
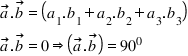
4. Tích có hướng của 2 véc tơ là 1 vec tơ, vuông góc với 2 vec tơ thành phần.


* Ứng dụng:
– Tính diện tích hình bình hành ABCD: ![]()
– Tính diện tích tam giác ABC: ![]()
– Tính thể tích hình hộp ABCDA’B’C’D’: ![]()
– Tính thể tích tứ diện ABCD: ![]()
– Chứng minh 3 điểm A, B, C thẳng hàng: ![]()
– Chứng minh 3 điểm A, B, C không thẳng hàng: ![]()
– Chứng minh 4 điểm A, B, C, D đồng phẳng: ![]()
– Chứng minh 4 điểm A, B, C, D không đồng phẳng (A, B, C, D là 4 đỉnh của 1 tứ diện):
![]()
- Góc giữa 2 véc tơ.
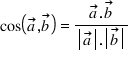
6. Tọa độ trung điểm của A, B.
– Cho hai điểm A(xA, yA, zA) và B(xB, yB, zB). Gọi M là trung điểm của AB, khi đó:
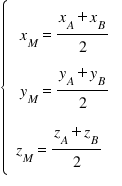
- Tọa độ trọng tâm tam giác A, B, C.
– Cho 3 điểm A(xA, yA, zA), B(xB, yB, zB), C(xC, yC, zC) . Gọi G là trọng tâm của tam giác ABC, khi đó:
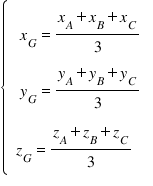
– Cho điểm m bất kỳ trong không gian, ta luôn có: ![]()
- Tọa độ trọng tâm tứ diện ABCD.
– Gọi G là trọng tâm tứ diện ABCD. Khi đó:

II. Một số dạng toán thường gặp sử dụng các công thức cần thiết của phương pháp tọa độ
Dạng 1: Các bài toán cơ bản( các yếu tố đã cho sẵn)
- Viết phương trình mặt phẳng đi qua ba điểm, đi qua một điểm và song song với mặt phẳng cho trước…
- Viết phương trình đường thẳng đi qua hai điểm, song song với đường thẳng cho trước…
- Chứng minh ABCD là một tứ diện, tính diện tích tam giác biết tọa độ ba điểm…
- Tìm tọa độ hình chiếu của điểm trên đường thẳng, mặt phẳng…
- Viết phương trình mặt cầu biết tâm và bán kính, đi qua 4 điểm đã cho…
Dạng 2: Bài toán về phương trình mặt phẳng và các vấn đề liên quan
- Viết phương trình mặt phẳng bằng cách xác định VTPT
- Viết phương trình mặt phẳng liên quan đến khoảng cách
- Viết phương trình mặt phẳng dạng đoạn chắn
- Viết phương trình mặt phẳng liên quan đến góc
- Viết phương trình mặt phẳng liên quan đến mặt cầu
- Các dạng toán khác về mặt phẳng
Dạng 3: Bài toán về phương trình đường thẳng và các vấn đề liên quan
- Viết phương trình đường thẳng bằng cách xác định VTCP
- Viết phương trình đường thẳng liên quan đến đường thẳng khác
- Viết phương trình đường thẳng liên quan đến khoảng cách
- Viết phương trình đường thẳng liên quan đến góc
- Viết phương trình đường thẳng liên quan đến diện tích tam giác
Dạng 4 : Các bài toán tổng hợp












